It’s not my intent to provide a complete course in how a computer chess engine is programmed. Most readers would find the topic pointless and maybe a little boring. But, to be able to make full use of a digital training and analysis partner, there are a few things that every player who uses a chess program needs to know about how a computer plays chess and analyzes positions. I promise to make this article as painless as possible and hopefully I can even make it a little bit entertaining.
So how does a chess engine work?
The Chess engine works by analyzing chess positions and generating a list of moves that are the strongest. The chess engine is a back end with a command-line interface with no graphics or windowing.
Chess Engine Tree Of Possibilities
Every chess position offers endless possibilities. Don’t believe me? Let’s set up a chessboard, take a look, and consider a few simple numbers.

- Yep, it’s the starting position for a game of chess. White has twenty possible moves at the game’s start (two for each of eight pawns and two for each of two Knights;
(16 + 4 = 20).
After any of White’s twenty possible starting moves, Black has twenty possible moves of his own. Thus there are 400 possible chess positions after just one move by each player (20 x 20 = 400). Four hundred possible positions after just one move for each side. Wow!
- Now let’s expand on that idea. Just as an example, we’ll imagine a position in which White has exactly thirty possible moves (we call each of these a candidate move), for each of which Black has exactly thirty candidate moves in reply, after each of which White has exactly thirty possible replies to each of Black’s moves, and so on.
Sure, it’s highly unlikely that a position that produces such nice orderly numbers exists, but that’s why I said we need to imagine it. Besides, the initial position isn’t the point. It’s the number of positions which come later.
So we’ll imagine that such a position exists. After White makes one move which computer chess guys call a “half move” or a “ply”, there are thirty possible new chess positions. After Black’s first reply, that number increases to exactly 900 possible positions. Assuming exactly thirty possible moves in each new board position, watch what happens to the numbers each time the players go one half-move (one ply) ahead:
| White’s first move | 1 ply | 30 positions |
| Black’s first move | 2 ply | 900 positions |
| White’s second move | 3 ply | 27,000 positions |
| Black’s second move | 4 ply | 810,000 positions |
| White’s third move | 5 ply | 24,300,000 positions |
| Black’s third move | 6 ply | 729,000,000 positions |
| White’s fourth move | 7 ply | 21,870,000,000 positions |
| Back’s fourth move | 8 ply | 656,100,000,000 positions |
I wanted to keep going, but black smoke started rolling out of my calculator. If you don’t believe the numbers, try it yourself (but quit when you see smoke). In our imaginary position, after just four moves for both players (eight plies, in computer chess terms), there are more than six hundred and fifty billion possible board positions, billions of combinations of pieces on the board.
So the next time you meet a strong chess player and he claims that he sees “everything” four moves ahead, you have my permission to say, “Liar, liar, pants on fire!” (And if you want his pants to really be on fire, do all of that multiplication on your calculator again and then stick it in his back pocket when he’s not looking.)
We call that big ol’ batch of potential moves the “chess tree”. And I’ll bet you’re dying to know why aren’t you? I’m glad you asked. Have a look at this (very small) example which occurs after the moves 1.e4 e5 2.Nf3 Nc6 3.Bb5 a6:
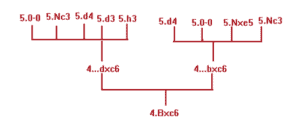
These are the initial moves of the Ruy Lopez Exchange Variation (and don’t worry if you can’t read algebraic chess notation. See How to write down chess moves in algebraic notation?
White plays 4.Bxc6 (that move is what makes it the Exchange Variation). Black has a lot of moves he can play next, but only two which make any real chess sense. White has a few good replies to both of Black’s moves. If we start reading the diagram at the bottom with 4.Bxc6, then add Black’s replies above it, then add White’s replies above Black’s, and connect them all with lines, we get something that looks very like a tree.
That’s why it’s called a chess tree and you’ll often hear chess variations called “branches”, and hear a position at the end of a variation called a “leaf node”. It’s a wonder that chess analysts aren’t called “gardeners”, for crying out loud.
Crunching The Numbers
When we talk about evaluating a chess position, we mean looking at the board with knowledge of which side is to move. That does make a big difference! and figuring out which player currently has the advantage.
We all do this all the time when we play chess. We look at the board, figure out who’s ahead, and then we start looking at candidate moves, figuring what the opponent might do in reply to each of them, then what we’d do next, and then we decide who’s ahead.“If I do this, he’ll do that, then I’ll do this, who’s ahead then?”).
It’s a little more complicated than this in actual practice, but when you get right down to it, that’s what we all do as we play. We assess the current position, look at candidate moves for both players (repeating this for as many moves ahead as we can envision), and then reassess the resulting positions. And while we’re here, do you want to know the big difference between how an average player evaluates positions compared to a grandmaster?
A grandmaster considers better candidate moves than the average player does. It’s pretty much as simple as that. Grandmaster Yasser Seirawan talks about this in the PBS Nova episode about computer chess. Chess computer engines basically do the same thing as humans, just a few million times faster, and by reducing the problem to a mathematical formula.
Post you may like: How to beat the computer at chess?
The Chess Engine Algorithm
A chess engine uses a complicated formula, called an algorithm, to evaluate a position. Going back to our chess tree example, a computer would look at the position after 4.Bxc6 and then refer to its algorithm to come up with a numerical evaluation of the position. Many chess factors are assigned numbers in the engine’s algorithm. These factors include really simple things, like material, who has more pieces on the board.
Other factors include space and mobility (whose pieces can move to, and thus control, more squares), pawn structures (factors such as pawn islands or backward and isolated pawns), King safety (is the opponent’s King in an exposed spot?), and scores of other similar chess ideas. Each factor is assigned a number by the programmer (and different chess programmers assign different values, which is why all chess engines don’t play chess the exact same way)
The numbers are plugged into the algorithm, the calculations are made, and BOOM! The position is assigned a numerical value, an evaluation of the position. In our example, the chess engine would look at the position after 4.Bxc6 and assign it an evaluation. Then it would move ahead one ply and evaluate every Black reply to 4.Bxc6. Then it would move ahead another ply and evaluate all of White’s responses to every possible Black move, assigning each new board position a numerical evaluation. And on and on, evaluating millions of positions a second (on present-day hardware).
But due to the size of the game tree, we considered earlier, even Houdini 2, evaluating 3 million positions a second on a home PC, would tend to bog down after just a few moves. Going way back to our chess tree example, in which four moves for each player result in over 650 billion chess positions, it would take Houdini 2 more than two hundred thousand seconds (over sixty hours) to look just four moves ahead if it had to consider every single position. That’s why chess engines prune the chess tree and, yes, that’s the actual technical term. Gardening again.
Moves that lead to positions that have a very bad numerical evaluation get cut from further consideration early on in the search, and the engine just stops considering them in the same way that a human player blows off a first move which immediately loses his or her Queen or Rook, and then doesn’t think about that move anymore.
Moving Backwards Down The Branches
After a chess engine has assigned evaluations to a lot of positions, it takes the evaluations of the leaf nodes (the final positions of variations) and moves them backward through the tree, assigning them to earlier positions in an attempt to find out which candidate moves lead to the biggest rewards (higher evaluations) and, conversely, which lead to the biggest losses (lower evaluations).
The engine, armed with this information, will steer toward the best possible outcome for it (by playing the candidate move which leads to that outcome) while avoiding the worst possible outcome. In practice, it’s a bit more complicated than this, but that’s basically how it works. Claude Shannon came up with this in his early computer science writings, and it’s still used in varying forms today. It’s known as a min-max system of evaluation.
When a chess program evaluates candidate moves in a position, it assumes the best possible play for both sides from that point it always assumes that the opponent will play the best possible move as part of min-maxing to arrive at a decision.
Summary- How Does A Chess Engine Work
To use a chess engine properly, you’ll need to remember just a couple of important things we’ve learned in this article. When an engine shows you its search depth, that is, how many moves ahead it’s looked, it expresses this value in half-moves or plies.
When a chess engine shows you a numerical evaluation at the end of a suggested variation, those moves reflect the best play for both sides in the chess engine’s judgment (computers never say “Maybe he won’t see it…”), and the numerical evaluation the engine assigns applies to for the board position at the end of the variation it shows.
Finally, the farther ahead a computer searches (we often say “the deeper the engine looks into the position”), the better and more accurate the evaluation will tend to be. That’s why the old 1970s and 1980’s chess computers often played such awful chess; their processors weren’t strong enough to look deeply ahead, and their primitive algorithms sometimes misevaluated positions.
Present-day chess engines are not only faster but smarter, too – the art of programming a chess computer has advanced a great deal over the years. Now let’s get to work making you a better chess player!
When a chess engine shows you a numerical evaluation at the end of a suggested variation, those moves reflect the best play for both sides in the chess engine’s judgment (computers never say “Maybe he won’t see it…”), and the numerical evaluation the engine assigns applies to for the board position at the end of the variation it shows.
Finally, the farther ahead a computer searches (we often say “the deeper the engine looks into the position”), the better and more accurate the evaluation will tend to be. That’s why the old 1970s and 1980’s chess computers often played such awful chess; their processors weren’t strong enough to look deeply ahead, and their primitive algorithms sometimes misevaluated positions. Present-day chess engines are not only faster but smarter, too – the art of programming a chess computer has advanced a great deal over the years. Now let’s get to work making you a better chess player!
Now that you know how a chess engine works, it’s time to analyze your games with it. Click here to learn from Grandmaster Igor Smirnov on how to analyze your games like a pro! (FREE 30 min+ course )






